EML 3222 Spring 2018 System Dynamics

FIULogo_H_CMYKsmaller
Department of Mechanical and Materials Engineering

This is Dr. Levy’s EML3222 System Dynamics Spring 2018 page

Florida International University is a community of faculty, staff and students dedicated to generating and imparting knowledge through 1) excellent teaching and research, 2) the rigorous and respectful exchange of ideas, and 3) community service. All students should respect the right of others to have an equitable opportunity to learn and honestly demonstrate the quality of their learning. Therefore, all students are expected to adhere to a standard of academic conduct, which demonstrates respect for themselves, their fellow students, and the educational mission of the University. All students are deemed by the University to understand that if they are found responsible for academic misconduct, they will be subject to the Academic Misconduct procedures and sanctions, as outlined in the Student Handbook.

Here is the (12/27/2017) updated syllabus for the course.

My office is in EC3442, and email address is levyez@fiu.edu

My tel. no. is 305-348-3643. My fax no. is department fax no. is 348-1932

TA is to be determined. Please bring your questions to me.

OFFICE HRS: Monday from 10am-12pm and Wednesday from 300-430pm

Photocopies of the 3 material selections relating to vibrations will be available in my office starting August 26. Please make up your groups and one of you come to my office to get the materials. Cost is $15 per set.

Please start reading the first and second section-Chapter 1 and 2 materials. I will be assigning examples out of those materials starting next week (1/10). So it would be to your benefit to come pick up the copies for your group.

Out of the photocopies of the first two selections do the following: Problems 1.7 to 1.10, 1.13, 1.16, 1.19, 1.22, 1.26, 1.27, 1.29, 1.31, 1.32, and 1.36. Please do these problems as Exam 1 will have similar problems. So it will be to your advantage to understand this material

This material and all the linked materials provided, except where stated specifically, are copyrighted © Cesar Levy 2018 and is provided to the students of this course only. Use by any other individual without written consent of the author is forbidden.

PLEASE USE THE WINDOWS MEDIA PLAYER TO VIEW THESE VIDEOS.

Here is Lecture 1 related video and here are the pages related to that video lecture: page 1, page2, example, page 3, page 4, page 5

Here is Lecture 2 related video and the pages related to the video: page 6, page 7, and page 8

Please make sure that you have the following information about second order systems, namely:

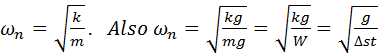where g is the acceleration of gravity and D_stis the static displacement of the system; that is, weight of the system = k*D_st.

And for systems with damping included: =2ςω_n and =ς and Ccrit=2mω_n =2√mk

Here is Lecture 3 related video: equation of motion for linear mechanical, linear rotational, inverted pendulum

Here is Lecture 4 related video: equivalent springs both linear and rotational, springs in parallel and series

Here is Lecture 5 related video: equivalent springs and masses using equivalent potential and kinetic energies

Here are solutions to some of the problems… problems 1-7 and 1-8, 1-9 and 1-10

Here are problems 1-13a and 1-13b, 1-29, 1-30, 1-35 and 1-35b

Here is Lecture 6 related video: we look at damped systems, derive equations and talk about overdamped, critically damped and underdamped systems

We have announced the first exam related to single degree of freedom systems, damped and undamped, for September 21. You will be allowed 2 pages 8.5 x 11 of formulas, but no solutions. This quiz is related to what we covered in class. A review of those topics are in videos 1-7.

Here is Lecture 7 video: we look at underdamped systems, derived logarithmic decrement and talk about two problems.

Look at Problems 2.1-2.4, 2.6, 2.7, 2.17 to 2.19, 2.28, 2.38, 2.45, 2.52, 2.60, 2.80, 2.82, 2.83, and 2.97. These are from the handout you obtained from the secretary’s office. . I will release the solutions on Sept 15 in preparation for your exam.

Now for underdamped systems: the logarithmic decrement, δ, equals 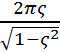where ζ is the damping ratio. NOTE δ IS NOT EQUAL TO D_st THE STATIC DISPLACEMENT

Also we showed that δ = (1/N) * ln(x_o/x_N) = (1/N) * ln(x_i/x_i+N)

where N = the number of cycles between the first and last measurement. x here is the displacement and the subscript “o” means the first measurement value. The formula also applies between any N cycles, meaning starting from cycle i and going to cycle i+N.

We will discuss the forced vibration of systems and cover the topic of resonance in a future lecture.

Here is Lecture 8 video: we now begin to look at forced vibration and derive the displacement function for a harmonic force F(t)=P sinw_ft. We discussed the effect of frequency ratio r=w_f/w_n and damping ratio ζ.

I am adding one more videotape in which problems on problems related to rotating unbalance and how to find the displacement due to forced vibrations Lecture 8a. Please see it before the second exam. The book from which the problems are taken are Vierck, Vibration Analysis.

This material and all the linked materials provided, except where stated specifically, are copyrighted © Cesar Levy 2016 and is provided to the students of this course only. Use by any other individual without written consent of the author is forbidden.

Please start reading Chapters 1 and 2 in the book by Rowell and Wormley.

Here is Lecture 9 video: we cover two problems, one forced undamped and one forced damped vibration problem. We then begin the topic of system dynamics by defining the through and across variables, the elemental and constitutive equations, the ideal and pure element. Here are the pages that go with the last part of the lecture: page 9, page10, page11, and examples,

As promised, here are the solutions to some of the problems assigned previously:

Here are problems 2-4, 2-6 and 2-7

Here are problems 2-17, 2-18, 2-19

Here are problems like 2-28, 2-38

Here is the rest of 2-38, and problems 2-68, 2-79

Here is problem 2-45

Here is problem 2-60

Here, the second problem is like problem 2.80

Here are problems the first two are like 2.83, 2.97

Even though I will not be here, THERE WILL BE A CLASS TOMORROW, Sept 21. I have asked Dr. Aravelli to substitute and teach the class tomorrow. You will be covering the forced vibration of a single degree of freedom system. She is very familiar with this material.

Tomorrow and the next set of lectures, please ensure that you bring the two handouts that I gave out at the end of the class on Wednesday.

Also, please look at the videotape for lesson 8 which reviews the materials related to Forced Vibration of a single degree of freedom system, either before or after. This material will be covered by your second examination.

Lastly, I will have office hours on Wednesday from 11-1230 if you have any questions.

Remember that the first exam is Sept 21 and that you are allowed 2 8.5 x11 inch formula sheets that deal with the materials we have spoken about from the beginning of the semester until the end of Wednesday's class. No Forced vibrations materials will be on the first examination.

I am attaching an extra video that I ask you to review that covers the topic of rotating unbalance Lecture 9a. The materials I want you to pay attention to begins from time marker 44:12 to the very end. Just before that section I do problems from the handouts I have given you. We will be doing some more problems from the handouts I gave you.

Please review the videos for the examination. We will pick up from the point where we left off today.

Our second exam will be on October 7 and will cover the materials related to single degree of freedom systems under forced vibration. That includes undamped systems under forced vibrations and damped systems under forced vibration; force transmitted to the support; rotating unbalance and the force transmitted to the support in the rotating unbalance case.

You will be allowed to bring 3 8.5 x 11 inch formula sheets—formulas only but no worked out problems.

We now begin the material from the Rowell and Wormley book on System Dynamics. Please read chapters 1, 2 if you haven’t done so already. We then begin the topic of system dynamics by defining the through and across variables, the elemental and constitutive equations, the ideal and pure element. Here are the pages that go with the last part of the lecture: page 9, page10, page11, and examples

Here is the material that goes with Lecture 13 video on rotational mechanical systems and transformers, both rotational and linear mechanical: page12, page 13, page 14, page 15, page 16.

Here is the material that will go with Lecture 14 video on transformers including rack and pinion: page 16, page 17, and continues on page 18, page 19, page 20, examples with electrical elements including transformers and transducers, examples with electrical elements 2, page 21

Due to Hurricane Matthew, the exam listed for October 7 was changed to October 12. It will cover the materials related to single degree of freedom systems under forced vibration. That includes undamped systems under forced vibrations and damped systems under forced vibration; force transmitted to the support; rotating unbalance and the force transmitted to the support in the rotating unbalance case. You will be allowed to bring 3 8.5 x 11 inch formula sheets—formulas only but no worked out problems.

The information on pgs 17-21 of Rowell and Wormley’s book deals with electrical elements: capacitors, inductors and resistors. They are like electrical “masses”, “springs” and “dampers”. The material will not be covered in class due to the cancellation of classes due to Hurricane Matthew, but you will be responsible for it. Review the videotape for Lecture 14 to cover the main elements, transformers and transducers. Just note the similar way we can describe electrical elements in comparison to linear mechanical and rotational mechanical elements.

Start reading chapter 6 on transducers in one energy domain (transformers) and transducers in multi energy domains (transducers)

Work on the following problems 1.1, 1.4, 2.2, 2.4 from your Rowell and Wormley books not the notes. Solutions will be posted in a week’s time.

Here are the pages that go with Lecture 15 on Fluid systems: page 22, page 23, page 24, page 25, page 26.

Please do problems 4.1, 4.2, 4.5 and 4.11 in your books. Their solutions will be revealed on October 26, 2016.

Here is the material that will go with Lecture 16 video: page 26, page 27, page 28, page 29, page 30,

Here is the material that will go with Lecture 17 video on thermal systems: page 30, page 31, page 32, page 33, page 34, example solution.

Here is the material that goes with Lecture 18 on linear graphs, as well: page 36, page 37, page 38, page 39, page 40, page 41, page 42.

Though I have uploaded what we will cover this week, I also plan to do some problems not covered in the videotapes. You will be responsible for those problems as well.

Here are the Problems 1.1, 1.4, 2.2, 2.4 and the solutions: problem 1, problem 2a 2b, problem 3a 3b, problem 4

Your second exam will be returned on Friday October 28 in class. Please be there to pick up your examination.

Here is the material that goes with Lecture 19 video: page 42, page 43, page 44, page 44solution,, page 45-46 examples, page 45-46solns

Here is the material that goes with Lecture 20 video: page 47, page 48, page 49, page 50, and page 51,

Here is the material that goes with Lecture 21 video: page 51, page 52, page 53, page 54,

Here is the material that goes with Lecture 22 video: page 54, These are the solution to page 54 top and bottom problems page 55, page 56. We also will cover page 57, page 58. Please note that the solution shown on pg 56 shows the result if the source is a Q source, not a P source as covered in class.

HERE are the solutions to PROBLEMS 4.2, 4.3, 4.6d and 4.11d

You are also suggested to develop the state equations for three problems -- the two problems on page 54 that we will discuss (and whose solutions will be provided on page 55 and 56 of the notes on the website) and problem 6.15 in your book.

We now begin talking about state equations.

I AM INCLUDING HERE TWO PDF FILES THAT MIGHT HELP YOU: ONE IS ON LINEAR GRAPHS AND ONE IS ON STATE EQUATIONS. THESE DOCUMENTS ARE THE PRECURSOR DOCUMENTS THAT LED TO THE BOOK SYSTEM DYNAMICS, AN INTRODUCTION, BY ROWELL AND WORMLEY.

We now begin talking about state equation solutions. This solution methodology depends on understanding matrices. For those who need a review of matrices, here it is.

Also look at the STATE EQUATIONS FILE which comes from your book to find more examples for deriving state equations. Please note that the figure numbers used in the file can be found at the end of the file.

Next exam is announced for November 16: materials related to getting system graphs, elemental, vertex, loop equations and determining state variables and state equations will be on exam. You will not be asked to put them in matrix format, just get the state equations. You are allowed 4 (four) 8.5 x 11 formula sheets for the second exam but NO solved problems or definitions on the sheets. You should also know some basic facts about the different systems we have discussed to include similarities and differences.

Here is the material that goes with Lecture 23 video: discussed state variables and how to get the state variable equations and how to solve state variable equations- page 57, page 58, page 59. Page 60 is omitted.

As a review of system graph and state equation derivations we looked at this problem. We also showed the state equation solution which is given in the top half of the page.

Here is the material that goes with Lecture 24 video: We discussed the following system including getting the system graph. We also showed the state equation solution which is given in the bottom half of the page. We gave a handout and obtained the system graph for a fluid system connected to a piston that was connected rotating wheel and discussed the solution for several problems on the same sheet.

Wednesday Nov 16: We will give out a handout in class starting the topic of numerical solution of these state variable equations given in page 61, page 62 (see lecture 24 tape at end).

Friday Nov 18: We continue our discussion of numerical solutions of the state equations in Lecture 25. The rest of the numerical solution of sets of first order differential equations will be discussed. A handout will be given in class on the Runge-Kutta method. The handout is from Applied Numerical Methods by James, Wilford and Smith, pages 339-345 and 351-353. We plan to look at several examples and how they could be used in the different numerical methods discussed, namely: Euler, Modified Euler, Runge-Kutta Second Order method, Runge-Kutta Fourth Order Method

We continue our discussion of numerical solutions of the state equations in Lecture 26. We worked on several problems (4^th order and 2^nd order RK methods).

Reminder Exam Nov 16: You are allowed 4 8.5 x 11 formula sheets. Materials to be tested for this exam are related to getting system graphs; elemental equations, vertex or node equations, loop or path equations.

Getting the state variable equations will also be on the exam but you do not have to get the matrix form of the state variable equations.

Note that numerical solution of matrix differential equations will NOT be on exam.

You should also know some basic facts about the different systems we have discussed to include similarities and differences for this examination, as well.

The last exam which will deal with numerical solution of differential equations will occur on November 30 (please note change). You are allowed 3 8.5 x 11 sheets of paper for the exam. This includes the Euler, Modified Euler, Runge-Kutta methods for both one first order state equation as well as multiple first order equations.

We will also cover the rest of the analytical method of solving the state equations which will be included in the final exam.

Here is the material that goes with Lecture 27-28: We review the discussion of the state variables and how to get the state variable equations and how to solve state variable equations analytically- page 57, page 58, page 59, then we start discussion of the analytical method solution page 61, page 62, page 63

As a way of understanding what will be covered in the analytical solution of the state equations, do the following problems:

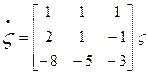Solve these and and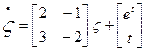

The solution to these problems will be revealed before the final exam.

Here is the material that goes with Lecture 28 video: We review finding the particular solution and how to deal with equal roots page 63, page 64 Another example for you to review on solution of matrix differential equation for the following matrix problem

how to handle the situation where the A-lI=0 leads to complex eigenvalues? Here is a document that gives an example of what to do.

Here is the solution to the matrix differential equation problems given previously– Problem 1 and 2, Problem 3.

REMINDER: Final exam will be on December 7 between 1200-200pm. Place will be EC1104

Please make sure you take care of your restroom needs before you start the exam. Minimize bringing munchies and drinks. There will be NO bathroom breaks.

It is a comprehensive exam that includes the vibrations covered at the beginning of class and the system dynamics. You will be allowed to bring in 8 8.5 x 11 in sheets into the examination. These sheets should be formula sheets only. Any sheets containing former exams of yours or others will be confiscated and you will forfeit the examination.

It is suggested that your 8 sheets contain the following:

1 sheet on the elemental equations; 1 sheet with the transformer/transducer equations,

2 sheets on vibrations related information; 2-3 sheets related to matrix/numerical methods, and 1 sheet of miscellaneous information you believe will help you.

Bring a working calculator and backup battery. Turn off all cellphones, iPODs.

Come in and take seats as we do with all exams.

Bring pens, pencils and erasers

I will provide exam and paper.

FOR THE FINAL! With respect to the sheet that you are allowed to bring into the exam in which you have your numerical methods formulas:

Please make sure you have the information for all the numerical methods we discussed either in class and/or in the numerical methods handout given in class, namely

1) Euler

2) Modified Euler

3) Runge-Kutta 2^nd order which is like the modified Euler

4) Runge-Kutta 2^nd order known as the midpoint method

5) Runge-Kutta 3^rd order

6) Runge-Kutta 4^th order

and how to use these methods if you have more than one state variable equation, as well.