 |
|||||
| Home | Research | For Teachers | HISTORY Level 1 Level 2 Level 3 |
PRINCIPLES Level 1 Level 2 Level 3 |
CAREER Level 1 Level 2 Level 3 |
| Gallery | Hot Links | What's New! | |||
| Web Administration and Tools | |||||
 |
|||||
| Home | Research | For Teachers | HISTORY Level 1 Level 2 Level 3 |
PRINCIPLES Level 1 Level 2 Level 3 |
CAREER Level 1 Level 2 Level 3 |
| Gallery | Hot Links | What's New! | |||
| Web Administration and Tools | |||||

WING-GRID, a Novel Device for Reduction of Induced Drag on Wings
U. La Roche, S. Palffy,
Fluid Mechanics Laboratory HTL Brugg-Windisch
CH-5200 Switzerland
Abstract
A new wingtip-device for reduction of induced drag on wings is reported. Relative reductions of induced drag compared to elliptical planar wing up to 50% have been verified.
The well known equation of Spreiter & Sacks for rolled-up vortex geometry has two parameters, that define the relative induced drag of any wing and wingtip configuration:
In the socalled Trefftz-plane behind a wing the trailing vortices have spacing and vortex-core radius. The contribution of a wingtip to increase the vortex-spacing and/or the vortex-core-radius for reduction of induced drag is used for the classification of wingtips.
Simultaneous exploitation of increasing vortex-spacing and increasing vortex-radius leads to configurations exceeding the potential of the known classic configurations by a wide margin.
Known is the Spiroid: published in Aviation Week of 6th December 1993 by Dr. Louis Gratzer.
Another is the WING-GRID treated in this paper. Both have been included in our windtunnel verifications and are identified to belong to the same class.
The paper reports the tests made and a preliminary description of the working principle of the wingtips belonging to this class as well as a description of the design information arrived at for the WING-GRID.
Introduction
As soon as the nature of induced drag was fully recognized, there was practically since WW1 an ongoing activity to reduce it. There is a very rich patent literature covering different approaches. A comprehensive compilation of the state of the art for 1983 was presented by H. Zimmer in [1].
At the time the following means to reduce induced drag on wings were known:
-planar straigth wings
-contouring plane wings
-simple wings with wingtip and endplates
-wings with slotted edges
-wings with fanned partial wings
With the classical categories of wingtips by H. Zimmer a focussed selection for their potential to reduce induced drag is not fully supported, since geometrical configuration criteria are used only. Specifically a focussed clarification of confi-gurations using multiple winglets was not achieved. In common of all the investigated configurations was, that somehow the verified effect always fell short of initial expectation.
Using as a tool to measure the effect of wingtips the Spreiter and Sacks theorem [2] giving vortex-spacing b' and vortex-core radius rk of the rolled up vortices as a function of induced drag we can see, that trying to reduce induced drag always influences two parameters.
1 widening spacing b' of the vortex-pair leaving the wing
2 widening the core-radius rk of the vortices
A natural tendency of the whole vortex-system is to react to a useful change of one parameter by increase or decrease of the other parameter in order to balance a given value of induced drag. An exemple in question is the rectangular wing, which with increasing aspect-ratio and increasing relative spacing b' of the leaving vortex-pair exhibits decreasing vortex-core radius rk in such a way as to retain as induced drag the equivalent value of an elliptic plane wing [3].
So only configurations have had success, where by one reason or another a net change over the sum of both the parameters spacing b' and vortex-core radius rk was accomplished.
By looking for a simultaneous effect on both parameters we arrive at better understanding of the problem and a new classification of different wingtips to reduce induced drag. And as a result we identify two new candidate configurations, the Spiroid and the WING-GRID.
Nomenclature
b span
b' spanwise spacing of vortex-pair
rk radius of vortex-core, e.g. Rankine vortex- core
Xell relative induced drag compared to plane elliptical reference wing
k relative induced drag expressed as 1/Xell
G circulation around wing profile
Go circulation in plane of symmetry
g dG/dy gradient of circulation along span
L total half-span of wing configuration considered
L2 partial span of wingtip-device
c chord winglets
t grid-interval
gap projection of grid-interval on free stream direction
a angle of attack of winglets
b orientation of grid = stagger angle
v free stream direction/velocity
Ca lift coefficient
Cwi induced drag coefficient
Cwi0 induced drag coefficient of (elliptic) reference wing
L aspect ratio, Lambda
n number of winglets in WINGRID or Spiroid
Re Reynoldsnumber
other to be found in the literature cited
From Helmholtz to Spreiter & Sacks
For a free-ended wing the theorem of Helmholtz applies, that the circulation leaving the wing is always equal to its value around the wing profile in the plane of symmetry. And in addition it states, that the particles of a vortex remain always the same. From the first is deduced in classical mechanical textbooks the description of induced drag as the kinetic energy in the vortices leaving the wings tip. The second statement explains, why we do observe a rolling up of the circulation leaving the wing some distance behind it.
As Betz [4] has shown, the center of gravity of the circulation leaving any wing is invariant and in the end identical with the center of the rolled-up vortices, for which Spreiter and Sacks [2] have shown the parameters describing induced drag to be the spacing b' of the vortex-pair and the radius rk of the vortex-core in the socalled Trefftz-plane far behind the wing, where the dispersed vorticity sheet leaving the wing is found as a rolled-up vortex.
[Fig. 1 Definitions Helmholtz]
An immediate application of the work of Spreiter & Sacks is Fig. 2.
In the diagram Xell, the relative induced drag of a wing configuration compared to a plane elliptical wing of the same span, is shown as a function of the two independent parameters b' and rk.
Fig. 2 is calculated with the explicit formula given in Fig. 3. It demonstrates, that for values of b'/b > 1 and increased vortex-core radius rk, Xell can go in principle as close to zero as a suitable wing configuration would allow.
Since we are only interested in reduction of induced drag, any nearfield-considerations of circulation-dispersial at the wingtip are not considered and are only relevant to our problem by the statement of Betz, that the center of gravity of the total circulation leaving the wing is invariant with distance behind the wing.
If the well known equation of Spreiter & Sacks is used as guideline two parameters define the relative induced drag of any wing and wingtip configuration:
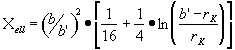
Fig. 3 Formula Xell
The equation also shows clearly, that the increase of rk does not increase the circulation value according to Helmoltz, it only does decrease the kinetic energy of the vortex.
According to the contribution of a wingtip to increase the vortex-spacing b' and/or the vortex-core-radius rk we arrive at a new classification of wingtips into four possible classes, Fig. 4:
1 Contour:
method to reduce induced drag is contouring a flat wing, e.g. by backswept wingtips increasing mainly vortex-spacing b'.(e.g. Dornier 228-wing)
2 Endplate:
adding endplates of various design at wingtip distributes circulation more at wingtip, again increasing vortex-spacing b'.(e.g. various retrofits of transport aircraft)
adding propellers has the same effects as end-plates, such a configuration tentatively being a member of the endplate-class (Airbus-study)
3 Open fanlike:
this configuration was up to 1993 the general class proposed to represent e.g. the working principle of soaring land-birds wings by having fanlike extensions of several winglets with open ends and at different orientations. Some successful and simplified wingtips (e.g. Whitcomb-type) in use belong to this class which works on increasing vortex-spacing and increasing vortex-radius, although with limited potential, e.g. U. Küppers [5].
4 Closed multiple:
This class is a fundamentally new configuration type opening the way to induced drag reductions exceeding the potential of the classes 1 to 3 by a wide margin, because both possible parameters for induced drag reduction are exploited together at the same time with the same purpose: see Fig. 3.
-increasing vortex-spacing b',
by circulation dispersal at wingtip
-increasing vortex-radius rk,
by distributing lift on several winglets individually
[Fig 4 Wingtip classification]
Class 4 operating principle
At the end of a long search for an explanation of the proper operational principle of a fanned multiple wingtip we tried out what would happen, if instead of using fanned winglets one would use parallel winglets. This was the configuration we were testing at first with mixed success, when at the same time the successfull full-scale tests of the Spiroid-device, invented by Dr. Louis Gratzer became known, published in Aviation Week of 6th December 1993 [6].
Having test results of a design belonging to the same class 4 helped very much to understand the operation of both configurations, the Spiroid and the WINGGRID.
The proposed wingtip-device has parallel fans or winglets. By this a transfer of the circulation from the main wing to the wingtip takes place not treated in the available references today, see e.g. [1], [3], [5] or [10].
[Fig. 5 Vortex shedding of wings]
As illustrated in Fig. 5 we have a special kind of doubledecker-effect at work (see also related concept of K. Wieghardt in [4]). The winglets positioned along the main wings edge take over its circulation segmentwise at the end of the main wing and by adding up their individual lift contributions they will produce essentially the the same lift per unit of span as the main wing section.
In order to do so, a minimum stagger angle is necessary, see Fig. 6. The minimum stagger-angle necessary is found to be dependent on the design angle of attack of the main wing and roughly of the same value. A further condition to assure the proposed circulation transfer is, that the winglets overlap (ratio of winglets chord to grid-spacing) should be smaller than 1 ( e.g. c/t < 1). In addition the winglets will be essentally parallel to each other in order to create the condition of a WING-GRID, where by grid-interference the transfer of the circulation to the end of the device is assured. The same effect without grid-interference is created in the Spiroid by the semi-spiral connection pieces of winglets with different dihedral orientation.
[Fig. 6 WING-GRID geometric definitions]
The deeper understanding of the devices operation developed along the following arguments.
C.D. Cone [3] did make an investigation based on the assumption, that the so called Munk-theorem would hold (measurements with potential-analogy-models). The measurements of H. Zimmer [1] however did not confirm this assumption.
Measurements with actual wings by H. Zimmer [1] resulted in a value for k = 0.85 which is equivalent to a Xell of 1.175.
We conclude from this discrepancy, that at wingtips we have a spatial circulation redistribution, which is not amenable to a treatment by assuming applicability of the Munk-theorem.
[Fig. 8 Summary operation class 4]
The estimated effect of the proposed WING-GRID device is proportional to the aspect-ratio of the individual winglets (distribution of lift on several winglets and proportional to relative span of the winglets compared to the span of the main wing). This was also verified for the Spiroid, see Fig. 11 and 12 below.
Windtunnel verifications
The verification of the effect of a wingtip-device with parallel winglets was based on:
-measurement of the polars (Ca^2 vs. Cw)
-measurement of increase of lift with geometric angle of attack. (Ca vs. alpha)
A further verification with the vortex-structure far behind the wing-model [2] did not succeed because of too short a downstream length of the windtunnel at disposal.
Windtunnel HTL experimental setup
The windtunnel installation used is a small tunnel with a cross-section of 0.8 on 0.5 meters and maximum velocity of 65 m/s. All measurements have subcritical Reynoldsnumber for the winglets chord. (Re < 200,000). With vortex-generators on the leading edge, see Chang [9], it was possible to get attached flow conditions for the selected con-figurations. This was also instrumental in achieving reproducible results.
Also two different configurations of the test-section allowed to compare the results of a preliminary estimation concerning windtunnel-corrections, see [8]. This check was used to establish validation of the results obtained for the elliptical wing used as reference.
[Fig. 9 Definition of windtunnel-configurations used]
The two windtunnel configurations used e.g. open vs. closed have been compared using the correction diagrams Fig. 6.28, (for very small models): curve B/D for open and curve A/C for closed configuration
The data used were, see Rae & Pope [8] pp 385 and 388 :
| Value | Symbol, data and formula |
| area of mirrored wing | S=.15*.85=.12 |
| cross-section test-section | C=.8*.5=.4 |
| factor S/C | S/C=.3 |
| Tunnel jet width-heigth ratio rectangular | r=.8/.5=1.6 |
| aspect ratio half-model | (b/2)/c=.425/.15=2.8 |
| correction open | d=-.2 |
| correction closed | d=+.1 |
Evaluation resulted in satisfactory agreement of the corrected polars closed and open despite the fact, that the corrections given are for small relative size of the model compared to the tunnel dimensions only, but are applied for a rather big relative size of the model.
Measurement apparatus
Balance: 6-component straingauge type of Flug-zeugwerke Emmen
Total pressure: Betz-manometer with pitot-tube
| Parameter | Value | Comment |
| half-span | 425 mm | half-model |
| span of wingtip-device | 125 mm | active span-length of winglets and/or Spiroid |
| ratio L2/L for comparison with device-hypothesis | 0.29 |
Geometrical wing-configuration
[Fig. 10 Measurement setup]
Continuous measurement of the downstream position of the trailing vortex center has been successfully used to verify the spanwise lift-distribution independently from the 6-component force measurements with balance, Fig. 10.
For correct operation of the wingtip-device a nearly rectangular lift distribution was attained by control of the relative angle of attack between main wing and wingtip-device set for a given configuration to be measured.
[Fig. 11 Expected and measured values of effect]
The value L2/L is the ratio of the span wingtip-device to total half-span including wingtip-device. Increase of apparent aspect-ratio is of cause simply the reciprocal value of the reduction of induced drag Cwi/Cwi0 expected.
Comments for evaluation
For evaluation of the inclination of the polars (Ca^2 vs Cw) the medium range of angle of attack only has been considered. (above small angles of attack and below flow-separation).
For evaluation of the increase of lift with geometrical angle of attack, see [4], the aspect ratio of the wing must be known:
L = 5.6.
Change of apparent aspect-ratio then can be written approximately as:
dL = f(dCa', L)
For evaluation we have to multiply the measured inclination-difference in the (Ca vs. a) diagram with the reciprocal value of the expression
d(Ca'/2p)/d(L) = 2/(L^2 + 4 * L + 4)
For an aspect-ratio L = 5.6 the left side expression has a numerical value of 29.
Results
The preliminary windtunnel-verifications did confirm operation of the WING-GRID and the Spiroid up to expectations based on the crude available model of its operation. However there are independent mea-surements known, were it was not possible to con-firm these results due to specific difficulties with the WING-GRID-configuration, which will be explained later.
A summary of the tests conducted at HTL is shown in Fig 12 below
As it is shown, the measured reduction of induced drag is in the range of up to 50% of Xell, the relative value compared to an elliptic planar wing of the same span. It is important to state which parameters were measured to establish the points in diagram Fig. 12:
1. value of Xell
2. value of b/b' by measuring the vortex separation of the rolled-up circulation (separation to windtunnel-wall that acted as a plane of symmetry of the model-wing). This also ensured, that the configuration in question did operate as a wing with near rectangular lift-distribution along the span, which is necessary for the WINGGRIDS effect to take place.
Other measurements carried out on this configuration apparently failed to duplicate this requirement. The WING-GRID configurations used in those tests invariably did not lead to the rectangular lift distribution necessary for various reasons:
-stagger angle too small in combination with winglets that have increased individual angle of attack from front to back
-small stagger angle combined with an overlap to big, so that the circulation of the main wing was not transferred individually to the winglets, the WING-GRID operating as a splitted wing.
-difficulty to reach the necessary lift with subcritical Reynoldsnumbers.
-using an already high aspect ratio test wing, which reduces the measurable net effect of induced drag roughly by the square of the aspect ratio.
Design
At the present stage of work a preliminary design procedure is available, Fig. 13
Based on the measurments and the insights on the operation of the configuration WING-GRID sofar, there are design information rules available giving answers to the following questions:
-What will be approximately the reduction of induced drag for given geometric parameters ?
-What are the geometrical limits for design parameters ?
-What will be the improvement for a given wing configuration ?
-How can different wings designs be compared?
It may be quite surprising to consider the calculated results comparing wings of equal glide-number and wing-load per area illustrated with the application of the device in the Fig. 14 below.
Proposed Applications
As a result of preliminary and conservative design studies we can illustrate proposed applications by the table below:
| aircraft type | aspect ratio geom. | induced drag % of total | % wing span with WING-GRID | reduction of induced drag | total drag reduction |
| DC-9-80 | 9.62 | 30% | 5% | 10% | 3% by retrofit elliptic wing |
| Maule MXT-7-180 | 6.2 | 50% | 5% | 50% | 25% by retrofit rectangular wing |
| UL-plane estimate | 6 | 60% | 20% | 70% | 42% by retrofit rectangular wing |
Conclusion:
-maximum effect results by application to rectangular wing,
-the gain on existing elliptic wings does not make full use of the potential for improvement, since there can not be a substantial gain on the small remaining circulation on the reduced chord-length at the tip.
Status of Work
international patents filed, further developement and prototype-work going on.
References
[1] H. Zimmer , the aerodynamic optimization of wings at subsonic speeds and the influence of wingtip design, NASA TM-88534 87 (translation of diss. Stuttgart 83)
[2] J.R. Spreiter and A.H. Sacks, the rolling up of the trailing vortex sheet and its effect on the downwash behind wings, journal of the aeronautical sciences jan.51, pp 21 uff.
[3] R. Staufenbiel and T. Vitting, formation of tip votices and vortex wake alleviation by tip devices, ICAS 1990
[4] H. Schlichting und E. Truckenbrodt, Aerodynamik des Flugzeuges, Teil 2, pp 9 uff., Springer 1969
[5] U.Küppers [5], Randwirbelteilung durch aufge-fächerte Flügelenden, Fortschr.-Ber. VDI-Z Reihe 7 Nr.8 1983 ISSN 0341-1753 )
[6] P. Proctor/Seattle, winglet designs to cut fuel burn, aviation week & space technology, Dec 6,1993 p 49
[7] C.D.Cone, the theory of induced lift and minimum induced drag of nonplanar lifting systems, NASA technical report R-139 1962
[8] Rae & Pope, Low-Speed Windtunnel Testing, John Wiley & Sons 1984, ISBN 0-471-87402-7
[9] P.W. Chang, separation of flow, pergamon press 1970
[10] A. de Jaco Veris, aircraft design concepts for reducing subsonic drag due to lift, aerotecnica missili e spazio, luglio-decembre 1992, pp 117-129
Send all comments to ![]() aeromaster@eng.fiu.edu
aeromaster@eng.fiu.edu
© 1995-98 ALLSTAR Network. All rights reserved worldwide.
Updated: 23 February, 1999