Sampling Theorem (Nyquist Theorem)

In order to allow exact reconstruction (back into the continuous time domain), an analog signal must be sampled at a rate greater than twice its highest frequency:

fs >= 2 x fmax

where: fmax  is the highest frequency component in the analog signal.

Note that this restriction assumes ideal conditions:
- Does not consider the presence of quantization errors
- Implies use of "Ideal LPF" for reconstruction

In practice, sampling rates larger than five times the maximum significant frequency component of the analog signal are recommended.

Frequency Domain Interpretation of Sampling Theorem:

Background:

1: The Fourier Transform reveals the frequency composition of continuous signals.

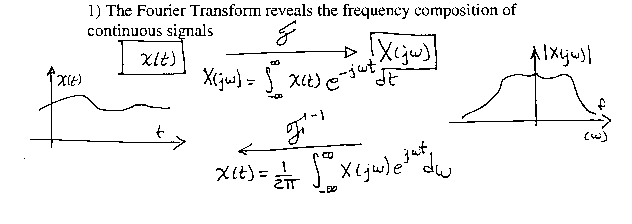
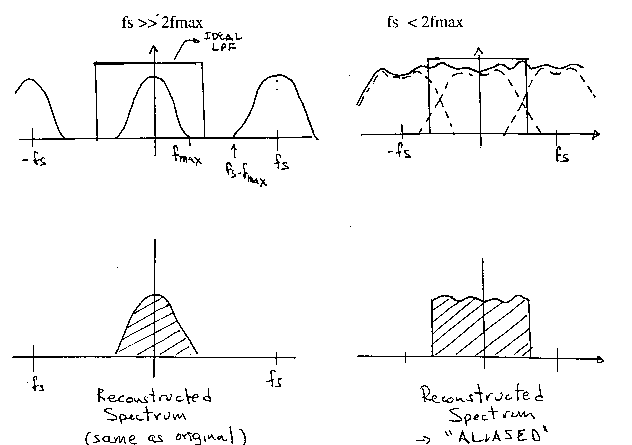
Recuperation of a continuous signal from a sampled signal is achieved by filtering (Low-Pass Filtering) the copy of the spectrum at low frequencies.

For a THEORETICAL best case, one can assume an IDEAL LOW-PAS FILTER.

Even in this ideal case the reconstructed signal will be distorted if the replicated spectra OVERLAP.  This distortion is called "ALIASING".

Back to Contents Menu