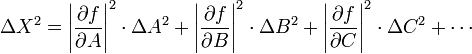Experimental Error analysis

Standard deviation:

Standard deviation is a measure of how much variation or "dispersion" there is from the "average" (mean, or expected value). A low standard deviation indicates that the data points tend to be very close to the mean, whereas high standard deviation indicates that the data are spread out over a large range of values.

Technically, the standard deviation of a statistical population or a data set is the square root of its variance. It is algebraically simpler though practically less robust than the average absolute deviation. A useful property of standard deviation is that, unlike variance, it is expressed in the same units as the data. Note, however, that for measurements with percentage as unit, the standard deviation will have percentage points as unit.

Sample standard deviation

The most common estimator for σ is the sample standard deviation, denoted by s and defined as follows:

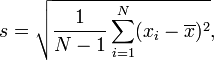
$s = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (x_i - \overline{x})^2},$

where $\scriptstyle\{x_1,\,x_2,\,\ldots,\,x_N\}$ are the observed values of the sample items and $\scriptstyle\overline{x}$ is the mean value of these observations. This estimation uses of N − 1 instead of N and tends to underestimate the population standard deviation. The term standard deviation of the sample is used for the uncorrected estimator (using N) while the term sample standard deviation is used for the corrected estimator (using N − 1). The denominator N − 1 is the number of degrees of freedom in the vector of residuals, $\scriptstyle(x_1-\overline{x},\; \dots,\; x_N-\overline{x})$ .

When you plot experimental data, the sample standard deviation may be plotted as error bars.

Propagation of error

In statistics, propagation of error (or propagation of uncertainty) is the effect of variables' uncertainties (or errors) on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations (e.g. instrument precision) which propagate to the combination of variables in the function.

The uncertainty (Δx ) is usually defined by the absolute error, here we can use sample standard deviation (s). The value of a quantity and its error are often expressed as x ± Δx.

Partial derivatives for error propagation:

Given $X=f(A, B, C, \dots)$ , then

Experimental error propagation
$\Delta X^2=\left \|\frac{\partial f}{\partial A}\right \|^2\cdot \Delta A^2+\left \|\frac{\partial f}{\partial B}\right \|^2\cdot \Delta B^2+\left \|\frac{\partial f}{\partial C}\right \|^2\cdot \Delta C^2+\cdots$

Where DA, DB, DC… are the sample standard deviation, s(A), s(B), s(C) … for measured variable A, B, C...

When you calculate modulus through the experimental data, you may need to determine the uncertainty.