
Department of Mechanical and Materials
Engineering
This is Dr. Levy’s EML3222 System Dynamics Summer 2010 page
Florida International University is a community of
faculty, staff and students dedicated to generating and imparting knowledge through
1) excellent teaching and research, 2) the rigorous and respectful exchange of
ideas, and 3) community service. All students should respect the right of
others to have an equitable opportunity to learn and honestly demonstrate the
quality of their learning. Therefore, all students are expected to adhere to a
standard of academic conduct, which demonstrates respect for themselves, their
fellow students, and the educational mission of the University. All students
are deemed by the University to understand that if they are found responsible
for academic misconduct, they will be subject to the Academic Misconduct
procedures and sanctions, as outlined in the Student Handbook.
Here is the modified (5/3/2010) syllabus for the course.
Class meets T-R from 200-315pm and F 1230-145pm starting 5/4 for 10 weeks. The final exam will be around 15 July and the date will be confirmed by the beginning of July.
My office is EC3474.
Office Hrs: M, T, R 330-5pm
My telephone and email: (305) 348-3643 (voice mail) and e-mail: levyez@fiu.edu
We will be learning some of the material that is found in the first chapter of Mechanical Vibrations by Singaresu S. Rao’s book related to vibrations. Please read the first chapter, Sections 1.4-1.10 and look at the first forty problems 1.1-1.40 by May 7. We will do some of them in class as we discuss the material. You will see that some of the basics of vibrations will also appear in system dynamics.
I will put at least one copy of the book in the library annex on the second floor by the Panther Pit. We will only need the book for that one chapter. It is not worth buying it for that one chapter.
Please start reading Chapters 1 and 2 in the book by
Rowell and Wormley. Download the notes
for the three lectures and be prepared to discuss them.
lecture 1: page 1, page2, example, page 3
lecture 2: page 4, page 5, page 6, page 7, page 8
This
material and all the linked materials provided, except where stated
specifically, are copyrighted © Cesar Levy 2010 and is provided to the students
of this course only. Use by any other
individual without written consent of the author is forbidden.
lecture 3: page 9, page10, page11, examples, page12, page 13, page 14
HW 1 is DUE May 18: Please do the following problems from the Rao handout (titled
Chapter 1 Fundamentals of Vibrations):
Problem 1.9, 1.13 (only equivalent spring constant), 1.27, 1.31 (only
equivalent spring constant), 1.36.
HW # 2 is due 5/21 Friday: Problems 1.1, 1.4, 2.2, 2.4 from your books
lecture 4: page 15, page 16, page 17,
The following information deals with electrical elements: capacitors, inductors and resistors.
They are like electrical “masses”, “springs” and “dampers”. Please read and understand.
The material will not be covered in depth in class but you will be responsible for it. I will skim over the material to cover the main elements, transformers and transducers. Just note the similar way we can describe electrical elements.
Lesson 5: The information on electrical elements begins at the end of page 17, and continues on page 18, page 19, page 20,
Start reading chapter 6 on
transducers in one energy domain (transformers) and transducers in multi energy
domains (transducers)
Lesson 6: examples with
electrical elements, examples with electrical elements 2,
page 21,
Lesson 7: page 22, page 23, page 24, page 25,
Problems from your book: problem 1, problem 2a 2b, problem 3a 3b, problem 4
lecture 8: page 25, page 26, page 27, page 28, page 29
lecture 9: page 30, page 31, page 32, page 33, page 34, example solution.
I include a copy of a videotape that covers thermal systems class
My office is EC3474. Office Hrs: M, T, R 330-5pm
lecture 10 page 35, page 35a, page 35b (note problem 2-23 here is like problem 6.1b in your book), page 36, page 37, page 38, page 39, page 40; Here is the tape as a review for this class,
HW2 solution: problem 1, problem 2a 2b, problem 3a 3b, problem 4
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
Read chapter 3 and chapter 4.
The first exam is Friday June 4. Insure that ALL
cellphones are off and that all bathroom requirements are completed prior to
the start of the exam. No one will be
allowed out of the classroom until the end of the exam and the exam has been
turned in.
The exam will consist of two
parts.
The first part is closed book. You should know similarities and differences
between systems. You should know the elemental
and constitutive equations for the different type elements. You should know across variables, through
variables, integrated across variables, integrated through variables for each
and every system. You should know how
systems and system elements can be defined, e.g., static, dynamic, stochastic,
and what kind of governing equations can be generated by different types of
elements involved in your system. You
should know how nonlinear elements can be linearized.
The
second part only allows the handout called appendix 2 modeling of
system elements that contains formulas for dampers, springs, inductances
etc. You will only be allowed to
take out the handout after part 1 has been collected. You will be asked to do some basic
computations and solve problems of the type given to you for homework.
lecture 11: page 40, page 41, page 42, page 43, page 44, page 44solution, Here is the same tape as a review for the first part of this class,
I will also be in my office on
Tuesday 6/1, Wednesday 6/2 for questions or by email. I will be in on Thursday 6/3 until about 5 pm for
questions you might have; or, you can contact me via email. My
office is EC3474. Office Hrs: M, T, R 330-5pm
Lecture 12: page 45-46 examples, page 45-46solns, page 47, page 48, I will be returning both your HWs in class on 6/3 -please be present to pick them up
Here are a set of problems which you do not have to turn in but you can do to see if you understand the materials. I also include the solutions, so that you can compare your results to the solutions posted.
Try 6.1b in your book to replace the system by an equivalent rotational system (i.e., find Jeq) and also replace the system by an equivalent linear mechanical system (i.e., find m eq). Also try problem 2.17 in your book. Finally, try problem 2.33 on the following pages page HW3prob3, page HW3prob3a
Here are the solutions to the above named problems: 1,
2, 3 .
Work out the results on your own first before you look at the solutions.
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
Lecture 14: page 49, page 50, page 51, page 52
HERE IS HOMEWORK 4.
PLEASE DO PROBLEMS 4.2, 4.3, 4.6d and 4.11d – FOR EACH OF THE PROBLEMS
DRAW THE SYSTEM GRAPH AND DERIVE THE CONTINUITY AND COMPATIBILITY EQUATIONS FOR
EACH. HOMEWORK IS DUE ON Tuesday 6/15.
Lecture 15: page 53, page 54, page 55, page 56, Here is a videotape
that covers the materials of the last two classes
Lecture 16: page 57, page 58. Here we will discuss state variables and how
to get the state equations.
HERE ARE SOME MORE EXAMPLES YOU CAN USE TO DERIVE THE
ELEMENTAL, NODE, PATH and STATE EQUATIONS ( 1
AND 2 ). These examples were discussed in class but
not in detail.
Lecture 17: page 58, page 59, page 60, page 61 see
bottom of page 58 for problem discussed on page 58/59.
For those who need a review of matrices, here it is.
I AM INCLUDING HERE TWO PDF FILES THAT MIGHT HELP YOU: ONE IS
ON LINEAR GRAPHS AND ONE IS ON STATE EQUATIONS. THESE DOCUMENTS APPEAR TO BE THE PRECURSOR
DOCUMENTS THAT LED TO THE BOOK SYSTEM
DYNAMICS, AN INTRODUCTION, BY ROWELL AND WORMLEY.
Also look at the STATE EQUATIONS FILE which comes from your book to find more examples for deriving state equations. At the end of the file you will find the figures mentioned in the FILE.
Lecture 20: page 61, page 62, page 63 ,
page 64 Here we will discuss solutions of the state
variables equations analytically. I
include a videotape
of the materials relating to the
solution to the matrix equations, both the solution to the transient and steady
state parts of the solution.
We also worked on problem 4.3
in the handout (Shearer and Kulakowski) given to you whose back side contained problems 7.29 and
7.30 .
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
You are given the following assignment (HW 5) due Tuesday 6/22: develop the state equations for problem 6.15 in your book. Also develop elemental/node/loop and system graphs for Figures 7.29 and 7.30 on the handout given to you Tuesday 6/15. This is a change to accommodate those with Summer A finals this week.
Also do the following problems for HW5, as well: Solve these ![]() and
and ![]() These are also due on Monday 6/22.
These are also due on Monday 6/22.
Lecture 21: The following problems (
1 AND 2 ) mentioned in previous lectures and
the following system graphs solution1 and solution2 and the following state
equation solution is given to you to look at and
understand. It is suggested that you do them by yourself
and compare to the given solutions.
We also briefly touched on the following matrix differential equation for
the following matrix problem ![]() . This problem is in your books on page 346 but I have
modified it by adding a non homogeneous term. The link leads to the solution of
both the homogeneous and non homogeneous part.
. This problem is in your books on page 346 but I have
modified it by adding a non homogeneous term. The link leads to the solution of
both the homogeneous and non homogeneous part.
We
also discussed the solutions to 7.29 and 7.30 in detail, especially the
transformer and transducer parts of the system graphs.
Please
read Chapter 5 on state equations and start reading Chapter 11 on numerical
solutions of differential equations.
Lecture 22: We will solve a simple heat transfer problem given in problems 4.14. and 5.20 in your books. We will also talk about the next exam and what materials will be covered on the exam. And we will start discussion of the numerical methods used to solve the state equations.
HERE are HOMEWORK 4 solutions. PROBLEMS 4.2,
4.3,
4.6d
and 4.11d
We also discussed
the solutions to 7.29 and 7.30 in detail in the last class, especially the
transformer and transducer parts of the system graphs.
Here is the solution to HW5 problem 6.15:
Problem 6.15
(a),
(b).
Here is the solution to the matrix problems for HW6 – Problem 1 was discussed in class on Tuesday 6/22. Here is the solution to Problem 2. The inhomogeneous term is different than the one given but the methodology is the same.
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
6/29, you are to form a team of 4: you are to choose a process that you can
model, with my OK. You will then be
asked to define the linear graph and get all equations as well as state
equations and you will be asked to solve the state equations for some
reasonable set of data.
Lecture 23: we will start numerical methods given in page 65, page 66, page 67 and a handout to be given and explained in class.
One of the students
asked about how to handle the situation where the A-lI=0
leads to complex eigenvalues. Here is a document that gives an example of what
to do.
Also, Please read the first two
sections of chapter 11 of your book on numerical methods.
We looked at several examples and
how they could be used in the different numerical methods discussed, namely:
Euler, Modified Euler, Runge-Kutta Second Order method, Runge-Kutta Fourth
Order Method and how Runge-Kutta can be used for systems of equations.
Lecture 24: We will start
discussion of the behavior of first order systems (such as a damper and spring,
or mass and damper) and second order systems (such as mass-spring-damper). Read Section 8.3, and Chapter 9. Here is some reading material from the
authors of your book that covers the topics we will touch on (First and Second Order response)
Lesson 25: exam 2: It
will be on July 8,
1- YOU WILL BE ALLOWED TO BRING IN: 7 8.5
X 11 SHEETS OF EQUATIONS BUT NO SOLUTIONS OF ANY KIND. BRING A WORKING CALCULATOR...YOU WILL NOT BE
ALLOWED TO BORROW ONE.
2- The materials that will be covered on the exam include:
LINEAR GRAPHS, SYSTEM GRAPHS, DERIVING COMPATIBILITY,
CONTINUITY, ELEMENTAL EQUATIONS, and STATE VARIABLE EQUATIONS. SO GIVEN A SYSTEM, YOU SHOULD BE ABLE TO
DERIVE THE SYSTEM GRAPH, THE CONTINUITY, COMPATIBILITY, ELEMENTAL EQUATIONS AND
THE STATE VARIABLE EQUATIONS.
3- YOU SHOULD ALSO BE ABLE TO SOLVE ANALYTICALLY (SUCH AS THE
HOMEWORK 5 ASSIGNMENT) MATRIX DIFFERENTIAL EQUATIONS OF THE FORM 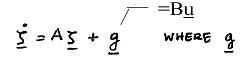
![]()
![]() .
.
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
4- PLEASE MAKE SURE YOUR EQUATION SHEETS INCLUDE THE MATERIAL
ON TRANSFORMERS AND TRANSDUCERS AS WELL.
5- NUMERICAL METHODS OF EULER AND MODIFIED EULER WILL
BE COVERED ON THIS EXAM.
Project Information:
You will be expected to produce
a project report by the 20th of July in a form similar to
your lab reports.
The report will include:
·
An introduction detailing what you are planning to model, who your team
members are and what they have contributed to the project;
·
Modeling section in which you give the modeling of your project and the
matrix form of those equations;
·
A results section in which you detail the numerical equations you will be
using to solve the problem, the parameters you will be using in your equations
and where they have been obtained, the graphs of the state variables as a
function of time, the outputs you want to find as a function of time;
·
and
finally a Discussion of your results. Also
discuss the step-size you use and its effect on the accuracy of the results
You will need to vary at
least 3 parameters to see the effect of parameter
variation on your solutions. Your discussion
section should be in depth.
In
all your projects you probably have one source (maybe more). Please take
one of the sources in the form A + B sin(omega*t) where A is the amplitude of
the source strength and B is the variation in the source strength and omega is
the frequency of the variation. Please vary at least one of these
variables; for instance you can take B as being 0.1 A, 0.3 A; or omega as being
some value between 0.5 pi to 2 pi.
Don't
forget to vary the parameters you were planning to vary before this additional
modification.
PROJECTS ARE DUE TO MY OFFICE
MANAGER’S OFFICE (EC3475) BY JULY 20 AT NOON. YOU MUST GIVE HER THE PROJECTS, NOT SLIDE
THEM UNDER MY DOOR. ITEMS SLID UNDER
MY DOOR WILL NOT BE EVALUATED AND THE TEAM THAT DOES WILL GET A ZERO; SO
PLEASE FOLLOW INSTRUCTIONS.
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
Lecture 26-27: In
lesson 26 we will cover the solution to the homogeneous part of the equation: ![]() , which is rewritten as
, which is rewritten as
![]()
Here are the pages dealing with what we will discuss on July 3 and what we will discuss on July 6. page 1, page 2, page 3, page 4. Note that you will have some materials covered in class (on overshoot, time constants and first order equations for example), that are not found in these sheets. Also, please compare your notes to these pages to insure that the same notation is used and that the variables are defined in the same manner.
Please do the following problems for HW 6 due on Friday July 9:
1-Do problems 8.9b and problem 8.18 all parts. Here the function us(t) represents
the Heaviside step function (=1 for t>0 and 0 for t<0).
2-Also do problem 9.8.
I have
also videotaped a class that covers several topics 1) a problem dealing with
system graphs; 2) what we talked about on Thursday July 1 and what we will be
talking about on Friday July 2; here it is
Please make sure that you have information about second order systems on your formula sheets, namely:
![]() =2ςωn and that
=2ςωn and that 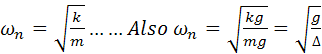 where g is the acceleration of gravity and
Δ is the
static displacement of the system; that is, weight of the system = k*Δ.
where g is the acceleration of gravity and
Δ is the
static displacement of the system; that is, weight of the system = k*Δ.
Now for underdamped
systems: the logarithmic decrement, δ, equals 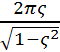 where ζ is the damping ratio.
where ζ is the damping ratio.
Also we showed that δ =
(1/N) * ln(vo/vN) = (1/N) * ln(vi/vi+N)
where N = the number of cycles between the
first and last measurement. v here is
the velocity and the subscript “o” means the first measurement value.
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
July 9, I did problem 9.23 in your books. Note that the solution is tending towards Vm =0.2
m/s which is the steady state solution of the problem due to the step increase
to Vm=0.2 m/s that occurs at t=0+. and here is the solution graph
Here are the solution to 8.9d and a problem not assigned in HW 6. You can pick up your homework when you turn in your projects. Projects are due on Tuesday July 20 by 12pm in my office manager’s room EC3475 (Mrs. Trasancos).
Here are solutions to 8.18
and 9.8
8.18a(i): t=2 and y=Ce-2t . Since y goes to zero as t increases, this is
stable. For (ii) t=-2 and y=Ce2t
. Since y goes to infinity as t
increases, this is unstable Please note these changes. They correct the error that t=1/2.
8.18b:
(i) when a < -1/4 the
solutions to the characteristic equation are complex. But the real part of the
solutions to the characteristic equation is negative, so the behavior is dying
oscillatory. Therefore the solution is asymptotically
stable in that the solution goes to zero as t increases, but it oscillates
while it goes to zero. The system is
underdamped.
(ii) When a=-1/4, the system
is critically damped; both solutions are dying exponentials and so the solution
to the ODE is stable.
(iii) When -1/4 < a < 0
both solutions to the ODE are dying exponentials and the solution is stable. This is an overdamped system since both rooms
of the characteristic equation are negative.
(iv) When a=0, the solution
to the ODE is unstable; one solution is a dying exponential but the
second is t which increases as t increases.
(v) When a > 0, both
solutions to the ODE are increasing exponentials; and so the solution to the
ODE is unstable.
8.18c: solutions are
sinusoidal and so the solution is neutrally stable as they oscillate
about the y=0 line.
9.8 has no state variable
since the velocity of the mass, v, is the same as the source, which is assumed
known for all time.
But, the governing equation
is (m/B) dv/dt + v = Fv(t)/B where -Fv(t) is the
conjugate variable to the source. Here
(m/B) is the time constant of the system.
To determine the time
constant for a first order equation, make the coefficient of function v =1 in
the equation (see previous paragraph), then the coefficient of dv/dt is the
time constant.
This material and all the linked materials
provided, except where stated specifically, are copyrighted © Cesar Levy 2010
and is provided to the students of this course only. Use by any other individual without written
consent of the author is forbidden.
To determine the time
constants (there are two) for the second order system:
Overdamped system: t=1/|s1| and 1/|s2|
Critically damped system: t=1/ωn
Underdamped system: t=1/ζωn
Final Exam is Friday
July 16, 1230-300pm in ROOM NHS 205
Don’t forget you will be allowed to bring in 10 sheets of 8.5 x
11 inch paper with whatever information you wish on it, except for solutions
from the book. I would suggest
you use the seven pages you had from the last exam and add 3 pages of helpful
materials you have gathered since then.
Materials from the last exam to the end will be emphasized but the exam
is comprehensive. Make sure you have a working calculator and that you
practice time management during the examination. Please make sure that you have information
about second order systems on your formula sheets-as explained above.
Note that the final exam is in
Room NHS205, not as I announced in class on Tuesday.
Reminder: Projects are due July 20
at 12pm in my office manager’s EC 3475.
Do not slide it under my door.
Project Information:
You will be expected to produce a
project report by the 20th of July in a form similar
to your lab reports.
The report will include:
·
An introduction detailing what you are planning to model, who your team
members are and what they have contributed to the project;
·
Modeling section in which you give the modeling of your project and the
matrix form of those equations;
·
A results section in which you detail the numerical equations you will be
using to solve the problem, the parameters you will be using in your equations
and where they have been obtained, the graphs of the state variables as a
function of time, the outputs you want to find as a function of time;
·
and
finally a Discussion of your results. Also
discuss the step-size you use and its effect on the accuracy of the results
You will need to vary at
least 3 parameters to see the effect of parameter
variation on your solutions. Your
discussion section should be in depth.
In
all your projects you probably have one source (maybe more). Please take
one of the sources in the form A + B sin(omega*t) where A is the amplitude of
the source strength and B is the variation in the source strength and omega is
the frequency of the variation. Please vary at least one of these
variables; for instance you can take B as being 0.1 A, 0.3 A; or omega as being
some value between 0.5 pi to 2 pi.
Don't
forget to vary the parameters you were planning to vary before this additional
modification.